Open your possibility with a no charge Alpha Brain trial!
Introduction. Who Owns Onnit Alpha Brain
In a globe that never quits, where our minds are continuously racing to stay up to date with the demands of contemporary life, cognitive improvement has come to be a luring mission. We’re all looking for that side, that additional mental boost that thrusts us to master our occupations, studies, and daily obstacles. This quest has given rise to a remarkable world of cognitive science and supplements, where the term “nootropics” preponderates.
Nootropics, usually referred to as “wise drugs” or “cognitive boosters,” have actually gained enormous appeal for their potential to develop our mental acumen and increase our cognitive expertise. And amid this vibrant landscape, one name sticks out as a leader and frontrunner Onnit Alpha Brain. Who Owns Onnit Alpha Brain
Open your possibility with a no charge Alpha Brain trial!
Introducing Onnit Alpha Brain.Who Owns Onnit Alpha Brain
Onnit Alpha Brain isn’t simply another item in the ever-expanding galaxy of nootropics. It’s a sign of innovation, a testimony to the ruthless quest of optimum psychological efficiency. So, why the buzz around this cognitive enhancer, and what sets it apart from the remainder? In this thorough overview, we embark on a trip to introduce the details of Onnit Alpha Brain.
We’ll explore its relevance in the nootropics market, dissect its components, and examine its potential to unlock your mind’s true potential.
Join us as we look into the heart of cognitive enhancement, exploring the world of Onnit Alpha Brain and just how it’s transforming the way we believe, focus, and overcome the difficulties of our hectic globe.Who Owns Onnit Alpha Brain
What is Onnit Alpha Brain?Who Owns Onnit Alpha Brain
Background and Manufacturer:
Onnit Alpha Brain is the brainchild of Onnit Labs, a popular business in the world of cognitive improvement and holistic health. Established by Aubrey Marcus, Onnit Labs has sculpted its niche in providing a variety of health and fitness items made to enhance human efficiency. Alpha Brain is just one of their flagship products, a testament to their devotion to opening the full potential of the human mind.Who Owns Onnit Alpha Brain
Key Selling Points:
Proven Solution: Alpha Brain isn’t just another mixture of untried components. It’s a diligently crafted blend of natural compounds, each selected for its potential to support cognitive feature.
Safe and Efficient: Safety and security is extremely important. Onnit Alpha Brain is made in a licensed center, sticking to stringent quality control criteria. This guarantees not just its safety but its effectiveness as well.
The Stalwarts of Recognition:
On the planet of cognitive enhancement, acknowledgment speaks quantities. Alpha Brain has garnered the attention and endorsement of noteworthy figures, including the prominent Joe Rogan. His recommendation of Alpha Brain has provided it a considerable increase in popularity.
Joining the Cognitive Elite:
Alpha Brain isn’t simply a supplement; it’s a movement. It’s a testament to the ever-evolving science of cognitive improvement and an essential player in this revolution. So, how did it get recognition, and what makes it attract attention in a market overflowing with choices? Allow’s explore even more as we study the core of Alpha Brain’s formula, components, and potential benefits.
Begin your Alpha Brain experience with a totally free trial!
Ingredients of Onnit Alpha Brain.Who Owns Onnit Alpha Brain

The true significance of Onnit Alpha Brain lies within its thoroughly selected components. Allow’s embark on a journey with the key elements of this cognitive enhancer.
1. Bacopa Monnieri: The Memory Mender
Bacopa Monnieri is an old-time natural herb understood for its memory-boosting residential or commercial properties. It supports cognitive functions by enhancing memory and decreasing stress and anxiety, making it a pivotal element in Alpha Brain’s formula.

2. Cat’s Claw: The Brain’s Shield
This Amazonian vine essence is a powerful antioxidant, protecting your brain from cost-free radicals and oxidative anxiety. It cultivates a healthy and balanced neural setting for optimum cognitive feature.
3. Oat Straw: The Cognitive Fuel
Oat Straw is abundant in vitamins, minerals, and antioxidants, supplying nutrition to the brain. It’s renowned for its possible to boost mental performance and cognitive efficiency.

4. L-Theanine: The Calm Catalyst
L-Theanine is an amino acid located in tea leaves, valued for its soothing impacts. It promotes leisure without inducing drowsiness, synergizing with other components for well balanced cognitive enhancement.

5. Alpha-GPC: The Neurotransmitter Dynamo
Alpha-GPC is a choline substance that plays a pivotal function in natural chemical manufacturing. It aids in improving memory, discovering, and cognitive clearness.
6. Huperzia Serrata: The Memory Amplifier
Extracted from the Huperzia plant, this component consists of Huperzine A, known for its role in memory renovation and cognitive improvement.

These active ingredients, diligently selected and blended, operate in consistency to produce a cognitive enhancer that intends to open your mind’s true capacity. Allow’s check out exactly how each component plays its part in raising cognitive function to brand-new elevations.Who Owns Onnit Alpha Brain
Does Onnit Alpha Brain Work?Who Owns Onnit Alpha Brain
The best litmus test for any type of cognitive enhancer is its effectiveness in enhancing psychological performance. Allow’s look into the scientific research, customer experiences, and the tangible advantages Alpha Brain needs to use.Who Owns Onnit Alpha Brain
supplement designed to enhance cognitive working in healthy adults, was examined through a rigorous randomized, double-blind, placebo-controlled test. The study involved 63 treatment-naïve individuals matured 18 to 35 that went through a 2-week placebo confrontation prior to getting either Alpha BRAIN ® or a brand-new placebo for a duration of 6 weeks. The participants underwent a battery of neuropsychological tests at the beginning and end of the research study, focusing on actions of postponed verbal recall and executive performance, in addition to rest patterns. The results revealed that Alpha BRAIN ® demonstrated substantial
improvements in delayed spoken recall and exec working contrasted to the placebo team. This research notes the very first randomized regulated trial of Alpha BRAIN ®, recommending appealing end results; nevertheless, additional research is necessitated to confirm and increase upon these findings.
From the National Library of Medicine https://pubmed.ncbi.nlm.nih.gov/26876224/
User Testimonials:Who Owns Onnit Alpha Brain
The true measure of any kind of item’s effectiveness lies in the experiences of its users. Across the globe, people have shared their success tales with Alpha Brain. These firsthand accounts supply important understandings into the item’s real-world impact.

The Substantial Benefits:
The appeal of Alpha Brain lies in the benefits it offers:
Enhanced Memory: Customers report enhanced memory recall and retention, making it an indispensable possession for students and specialists alike.
Laser-Like Emphasis: Alpha Brain is understood for developing focus and focus, helping in jobs that demand unwavering attention.
Psychological Quality: Experience clarity of thought, improved analytic, and improved cognitive dexterity.
Alpha Brain does not simply promise cognitive improvement; it provides on those promises. It’s the tool that encourages you to deal with life’s challenges with steadfast mental acumen. In the next area, we’ll explore the safety and security and safety measures to guarantee you make the most of this cognitive booster without concession.
Possible Adverse Effects and Safety And Security.Who Owns Onnit Alpha Brain
Prior to delving right into any cognitive enhancement journey, it’s essential to be aware of possible side effects and just how to make use of Onnit Alpha Brain safely.
Possible Side Effects:
While Onnit Alpha Brain is generally well-tolerated, some people may experience light negative effects. These can include migraines, nausea or vomiting, or digestive system pain. It is very important to comprehend that individual reactions can vary, and these effects are normally short-lived.
Consult a Medical Care Specialist:
Before incorporating any type of brand-new supplement right into your everyday regimen, it’s recommended to get in touch with a healthcare specialist, particularly if you have pre-existing clinical conditions or are taking various other drugs. Your healthcare provider can supply individualized guidance to make sure safety and security.
Tips for Safe Usage:
- Follow the recommended dosage provided on the item label.
- Avoid surpassing the recommended daily consumption.
- Keep hydrated to maximize the impacts of Alpha Brain.
- Monitor your feedback and readjust dose as required.
Security ought to constantly be a top priority. Understanding prospective adverse effects and getting in touch with a healthcare expert makes certain that you can appreciate the advantages of Onnit Alpha Brain without jeopardizing your well-being. In the next section, we’ll explore how Onnit Alpha Brain compares to other cognitive enhancers, giving insights right into its distinct staminas.
Experience cognitive enhancement-pick up your absolutely free trial right now!
How to Utilize Onnit Alpha Brain.Who Owns Onnit Alpha Brain
Maximizing the benefits of Onnit Alpha Brain needs precision in its usage. Allow’s explore the optimum means to integrate it into your day-to-day regimen.
Clear Dose Instructions:Who Owns Onnit Alpha Brain
The suggested dosage of Onnit Alpha Brain is usually laid out on the product label. It’s vital to stick to these directions. Typically, it’s recommended to take 2 capsules in the early morning to start your cognitive enhancement trip.
Time It Right:
Morning consumption is often recommended to line up with your body’s natural body clocks. This guarantees that you experience boosted emphasis, memory, and quality when you need it most throughout the day.
Keep Constant:
Consistency is key to profiting of Onnit Alpha Brain. Establish an everyday regimen, and stay with it to allow your body to adjust and enhance its results.
Hydration Matters:
Appropriate hydration is essential for cognitive function. Drinking an appropriate quantity of water can boost the effectiveness of Onnit Alpha Brain.
By following these usage guidelines and embracing consistency, you’ll harness the complete possibility of this cognitive enhancer. In the adhering to section, we’ll analyze just how Onnit Alpha Brain stacks up against its counterparts on the planet of cognitive improvement.
Contrasting Onnit Alpha Brain to Alternatives
Nootropics can be found in all sizes and shapes, and it’s important to recognize exactly how Onnit Alpha Brain stands out among the crowd.Who Owns Onnit Alpha Brain
Alpha Brain vs. Similar Nootropics:
Unique Formula: Onnit Alpha Brain is differentiated by its exclusive mix of components. While numerous nootropics share typical components, Alpha Brain’s certain formulation sets it apart.
Security First: Onnit Labs focuses on safety and quality control, guaranteeing that Alpha Brain is produced in a certified facility. This dedication to safety is an one-of-a-kind marketing point.
User-Backed: The abundance of customer testimonials and recommendations from prominent numbers like Joe Rogan speaks quantities concerning Alpha Brain’s efficiency and reliability.Who Owns Onnit Alpha Brain
Advantages of Onnit Alpha Brain:
Diverse Advantages: Alpha Brain offers a comprehensive range of cognitive advantages, varying from memory enhancement to boosted focus and mental clarity.
Clinically Validated Active Ingredients: The vital elements of Alpha Brain are backed by scientific research study, assuring their efficiency.
Quality control: Onnit Labs’ devotion to quality assurance makes sure that each dose is consistent and safe.
Understanding how Onnit Alpha Brain contrasts to its alternatives is vital when making a notified decision regarding your cognitive improvement trip. In the following section, we’ll check out customer evaluations and experiences, offering real-world understandings right into the item’s efficiency.
———————keep spintaxing from here———————-
Where to Acquire Onnit Alpha Brain
To start your journey with Onnit Alpha Brain, you need to recognize where to discover this cognitive enhancer and possibly obtain the very best bargains.Who Owns Onnit Alpha Brain
Official Site:
The official Onnit site is frequently the most reliable source for acquiring Onnit Alpha Brain Right here, you can be guaranteed of item credibility and high quality. In addition, Onnit’s main web site may provide special discount rates and promos for newbie buyers or faithful clients.
Accredited Merchants:
Some authorized stores may lug Onnit Alpha Brain, offering convenient choices for acquisition. It’s a good idea to verify the authenticity and track record of the seller to guarantee you’re getting an authentic product.
Online Marketplaces:
Popular online industries like Amazon may have Onnit Alpha Brain offered for purchase. However, exercise caution when buying from third-party sellers, and read reviews to guarantee you’re obtaining a genuine item.
Membership Solutions:
Onnit often offers membership services that can offer regular deliveries of Alpha Brain at affordable rates. This alternative is convenient for those that prepare to utilize Alpha Brain continuously.
Discount rates and Promos:
Watch out for price cuts and promos on the main site or via accredited sellers. These can provide cost-effective methods to start your cognitive enhancement journey.
Choosing the right area to acquire Onnit Alpha Brain is crucial for ensuring item authenticity and dependability. In the next area, we’ll conclude this ultimate overview, summing up essential takeaways and the transformative capacity of cognitive improvement with Onnit Alpha Brain.
User Reviews and Testimonials.Who Owns Onnit Alpha Brain
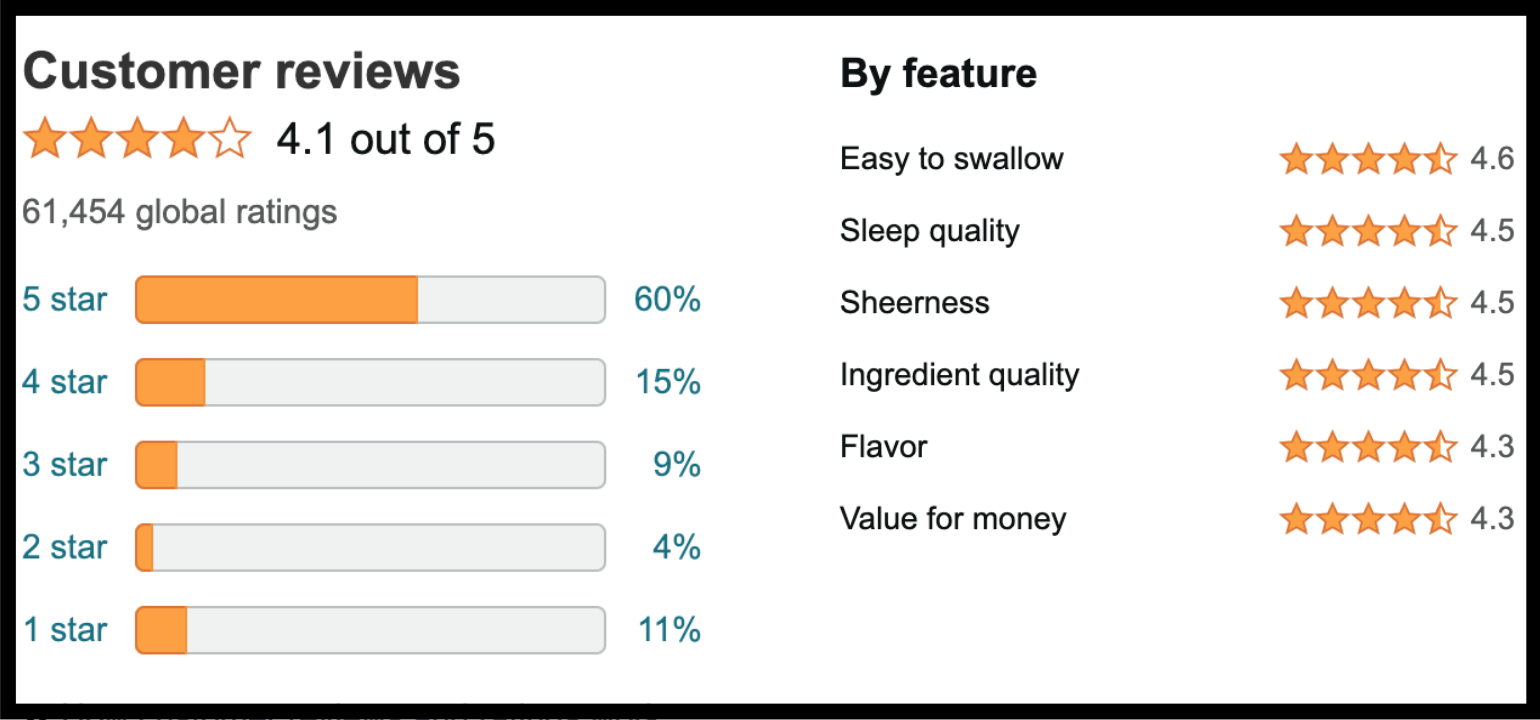
The real measure of a product’s worth lies in the experiences of those who have embraced it. Here, we share the voices of individuals who have journeyed with Onnit Alpha Brain.
Positive Experiences:
“Alpha Brain has transformed my workday. I can focus like never before and breeze through tasks.”
“Improved memory and mental clarity, which has been a game-changer for my studies.”
Balanced Perspectives:
“While I experienced a significant boost in focus, I did notice some mild initial headaches. However, they disappeared after a few days.”
“The effects of Alpha Brain were gradual, but I appreciate its subtlety. It helps me maintain a steady level of focus throughout the day.”
Negative Experiences:
“Unfortunately, Alpha Brain didn’t work for me. I didn’t experience any noticeable cognitive improvements.”
“I experienced digestive discomfort with Alpha Brain, which was a downside for me.”
These voices echo the real-world impact of Onnit Alpha Brain. As we end this best guide, we’ll summarize vital takeaways and reiterate the transformative potential of cognitive enhancement with Alpha Brain.
Conclusion.Who Owns Onnit Alpha Brain
In this detailed overview to Onnit Alpha Brain, we have actually navigated with the complex globe of cognitive enhancement and checked out the transformative capacity of this impressive nootropic.
Main Takeaways:Who Owns Onnit Alpha Brain
Onnit Alpha Brain, crafted by Onnit Labs, stands as a sign of development in the world of cognitive enhancement.
Sustained by clinical research study and user testimonies, Alpha Brain supplies tangible benefits, consisting of enhanced memory, focus, and psychological clearness.
Safety and security and liable usage are vital; it’s advisable to speak with a medical care professional prior to incorporating Alpha Brain into your regimen.
By adhering to suggested dose standards and preserving uniformity, you can take full advantage of the possibility of Alpha Brain.
The Transformative Power of Cognitive Improvement:
In today’s fast-paced globe, the mission for cognitive quality is a lot more appropriate than ever before. Onnit Alpha Brain offers a way to unlock your mind’s real possibility, equipping you to tackle life’s challenges with unwavering mental acumen.
Make an Informed Choice:
As you start your journey with Onnit Alpha Brain, we motivate you to make informed decisions. Assess your personal objectives, get in touch with medical care specialists when needed, and think about the transformative possibility that cognitive enhancement can supply.
Alpha Brain isn’t simply a supplement; it’s a key to unlocking your cognitive capacity, and improving your focus, memory, and psychological clearness. It’s your key to a world of unlimited opportunities.
In your search of cognitive quality, may Onnit Alpha Brain be the key that unlocks the doors to your maximum possibility.Who Owns Onnit Alpha Brain
What to do following
As you embark on your journey to explore the infinite potential of cognitive enhancement with Onnit Alpha Brain, we welcome you to proceed your pursuit for expertise and optimization.
Check out More on Our Blog:
For even more comprehensive information regarding nootropics, their benefits, and the ever-evolving globe of cognitive improvement, we motivate you to discover other articles on our blog site. Each short article explores one-of-a-kind aspects of cognitive performance, supplying insights and assistance to improve your psychological acumen.
Remain Upgraded with the Latest Fads:
To guarantee you’re always aware regarding the current nootropic patterns, innovations, and exclusive deals, we invite you to subscribe to our newsletter. Our newsletter is your entrance to a globe of cognitive excellence, providing you the essentials to unlock your complete potential.
Your cognitive trip has only just begun, and we’re here to lead you every action of the way. Subscribe now and maintain pushing the borders of your mind.
Thank you for choosing to optimize your cognitive possibility with us. With each other, we’re reaching new elevations in the quest of excellence.
Experience cognitive improvement-claim your completely free trial run now!
